Heimdallr

In order to calculate our Semi-Major Axis (average distance from the orbited star), we must first calculate the inner and outer bounds of our habitable zone:

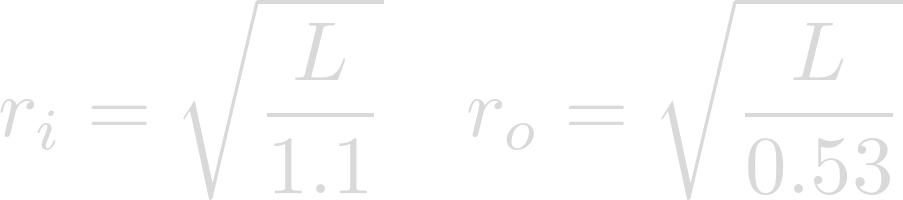
L is the luminosity of the orbited star in Solar units. Let's plug in Lich's luminosity for L.

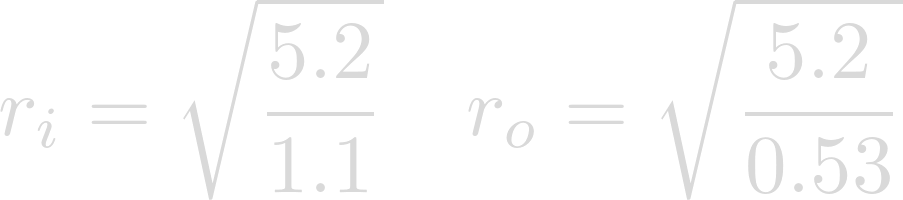
After evaluating we get our habitable bounds in Astronomical Units.

Our planet can lie anywhere within these bounds. I chose the following:

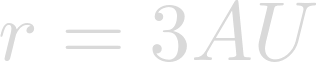
3 AU is near the outer limits of Lich's habitable zone, but it won't be an issue. Lich is very radioactive, and can therefore supply much of its own heat.

In order to calculate orbital period we utilize the following equation:

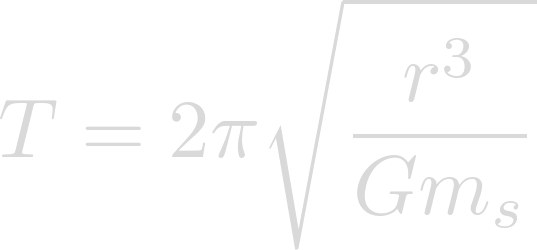
Now we can plug in our semi-major axis for r, the gravitational constant for G, and the mass of our star for m.

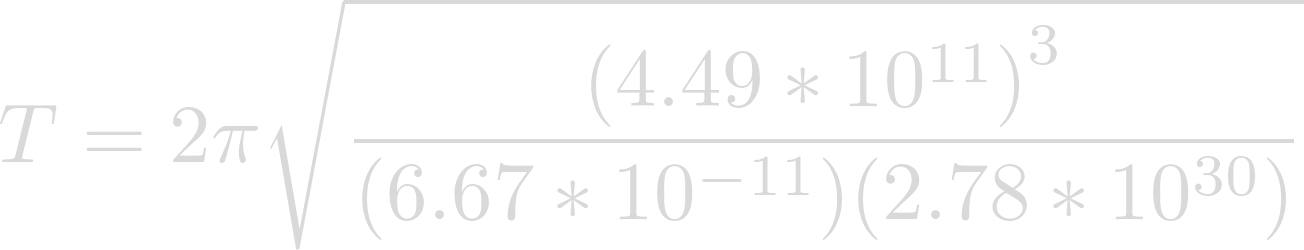
Evaluating the expression yields the orbital period of our planet.

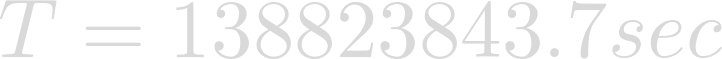
While we have technically found the orbital period of Heimdallr, this number, given in seconds, is not particularly useful — not to mention difficult to imagine. To obtain a more useful number, let's convert to years.

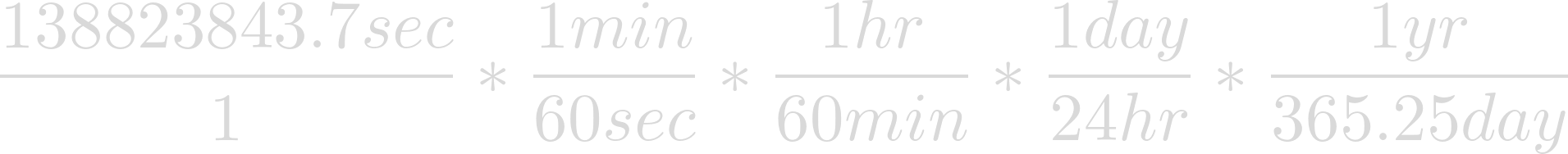
Now we have the orbital period of Heimdallr in years.

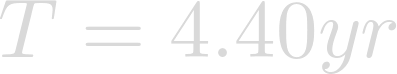
That is a much more descriptive number! We can now see that one year of Heimdallr is more than four earth years. This makes sense as Heimdallr is much farther from its star than Earth is from the Sun.

In order to find the acceleration of gravity on Heimdallr, we must find its gravitational field. We will start with the law of universal gravitation.

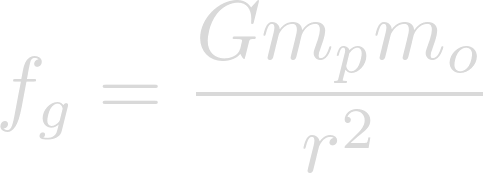
We can expand force to be mass times acceleration.

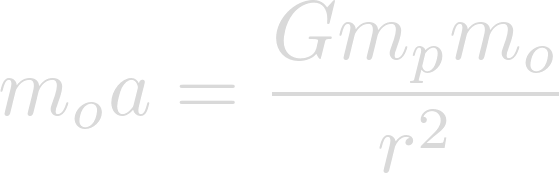
Now we can cancel the masses of the object and we are left with the equation for calculating a large object's gravitational field.

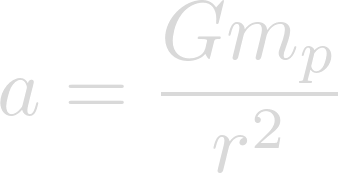
Now we can plug in our known values. The gravitational constant for G, the mass of Heimdallr for m, and the radius of Heimdallr for r.

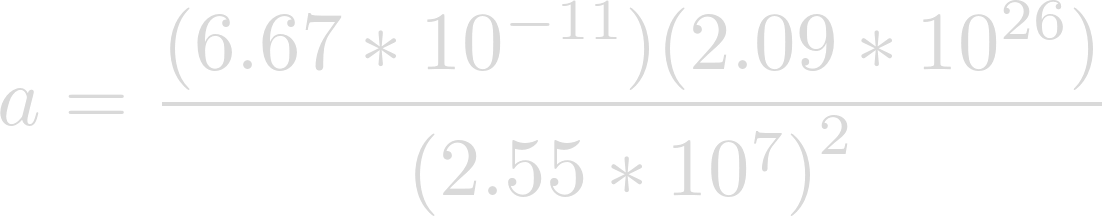
Evaluating yields the acceleration of gravity on the surface of Heimdallr.

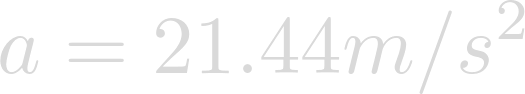
While Heimdallr is slightly less dense than earth, its radius is four times that of Earth and is therefore much more massive. This, in turn, results in the presence of a stronger gravitational field.

The orbital velocity of a planet can be solved for using the following equation:

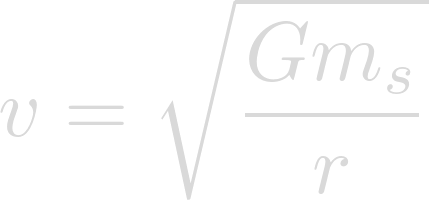
Now we can plug in our known values. The gravitational constant for G, the mass of Lich for m, and the semi-major axis of Heimdallr for r.

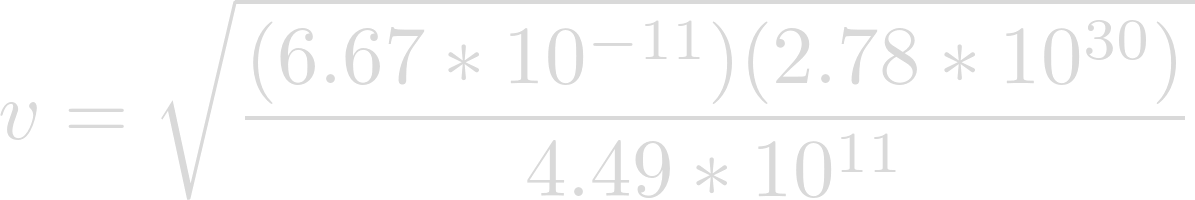
Evaluating yields the velocity at which Heimdallr is orbiting Lich

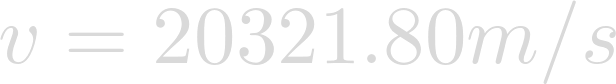
Since Heimdallr orbits farther from its star, it would make sense that its orbital velocity would be less than a planet closer to its star, like Earth

To find the rotational velocity at which objects on the equator would experience weightlessness, we need to find where the centripetal force required to keep objects on the surface is equal to the force of gravity. Centripetal force can be found using the following equation:

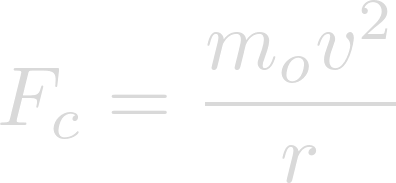
And gravitational force can be found using this equation:

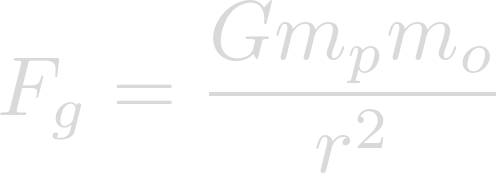
Where these two forces are equal, there are no perceived effects of gravity.

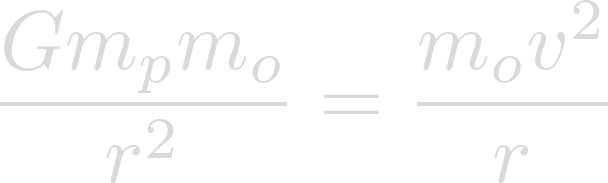
Now we can cancel the masses of the objects being rotated.

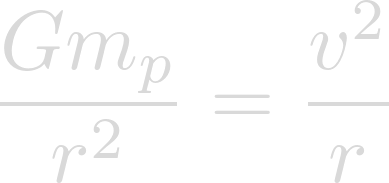
And the radius of Heimdallr...

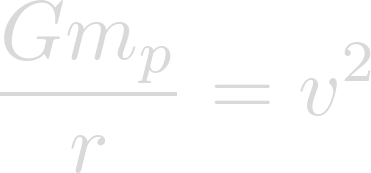
Finally we isolate velocity.

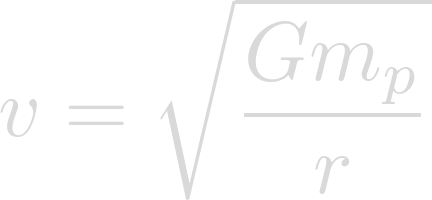
Now we can plug in our known values. The gravitational constant for G, the mass of Heimdallr for m, and the radius of Heimdallr for r.

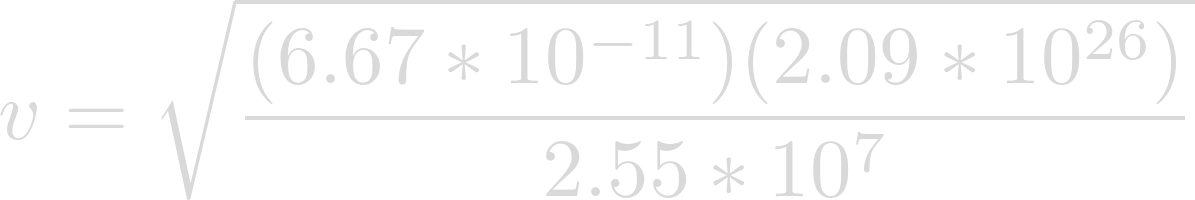
Evaluating tells us the velocity at which objects on the equator must be moving in order to experience weightlessness.

Helpful, but we want to know the rotational period of Heimdallr.

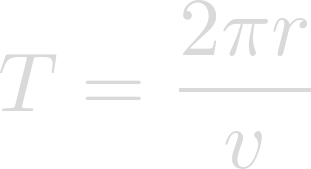
Plug in the radius of Heimdallr for r and the desired rotational velocity for v.

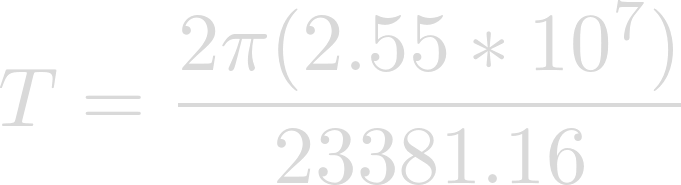
Evaluating yields the rotational period in seconds.

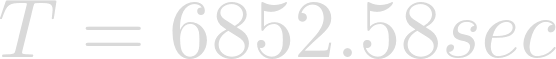
To make things easier to comprehend, let's convert.

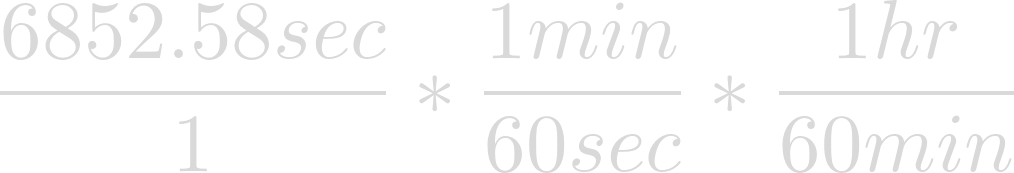
Finally evaluation yields the rotational period of Heimdallr in hours.

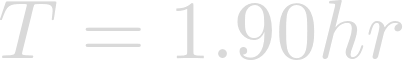
As one can tell from the rotational period Heimdallr, the planet is rotating very quickly. It is this rapid rotation that leads to Heimdallr's fascinating fluctuations in gravitation.

Now that we know that rotational period of the planet, why don't we develop an equation for determining the acceleration of gravity at any given latitude? Here is the equation for determining the rotational velocity of an object at any given latitude:

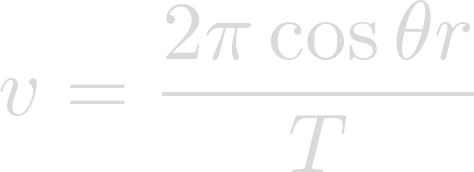
We also know that the equation for centripetal acceleration is:

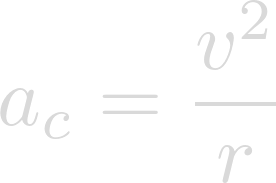
And that the equation for the acceleration of gravity is:

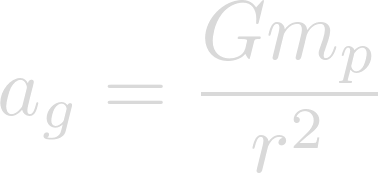
Since the imaginary centrifugal acceleration takes away from gravity, lets subtract the centripetal acceleration from the acceleration of gravity in order to find the net acceleration on the surface.

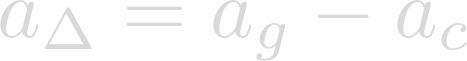
In order to put acceleration in terms of latitude, we can substitute our centripetal acceleration equation into the net acceleration equation.

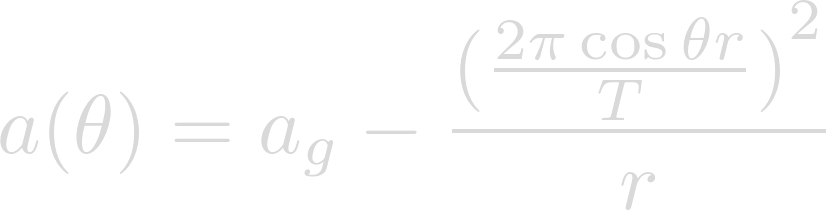
We can reduce the stacked fractions and distribute the squared over the velocity equation.

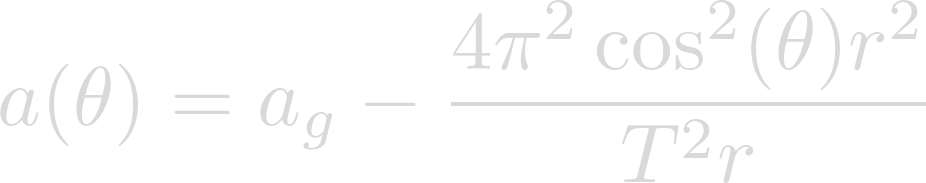
Finally we can simplify and obtain the final form of our equation.

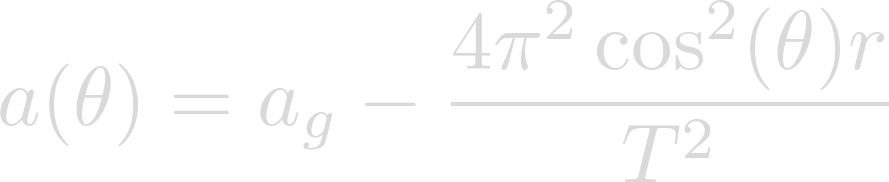
This function can be used to determine the gravitational acceleration at any given latitude. It can be used, for example, to determine that Heimdallr mimics earth gravity at a latitude of 42.5 degrees.

In order to explore the increased power of the Coriolis Force on Heimdallr, we'll calculate what the wind speed of Hurricane Katrina would have been if it had occurred on Heimdallr rather than on Earth. This equation yields the absolute angular momentum of a tropical cyclone:

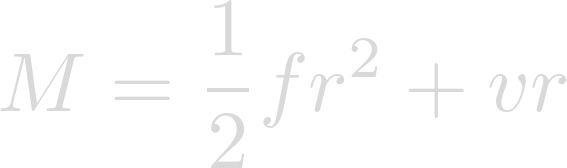
The variable in this equation that would differ on Heimdallr is f, the Coriolis Parameter, given by the equation:

Omega is the rotation rate of the planet in radians per second:

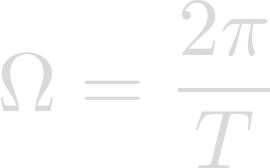
Phi is the latitude of the center of the storm. In the case of Hurricane Katrina, the latitude was:

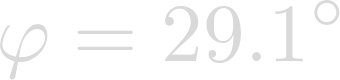
Plugging in Omega and Phi we have:

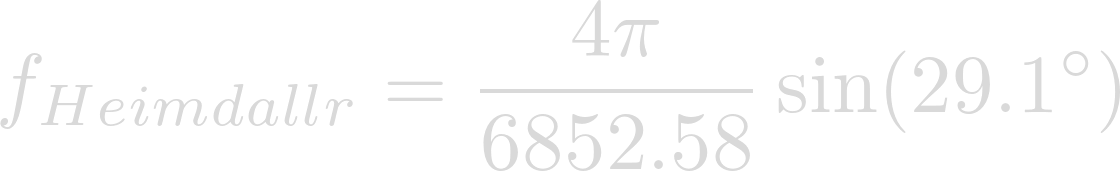
Evaluation yields the Coriolis Parameter on Heimdallr.

For the sake of comparison, let's plug Earths rotational period into the equation as well.

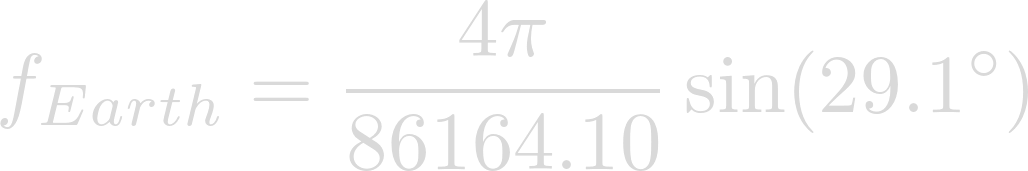
Evaluation yields the Coriolis Parameter on Earth.

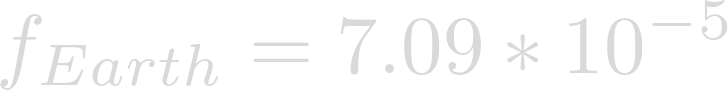
We can see that the Coriolis Parameter on Heimdallr is bigger than the Coriolis Parameter on Earth, but how much bigger?

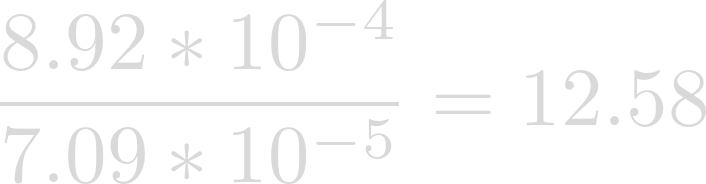
Now we can write a proportion:

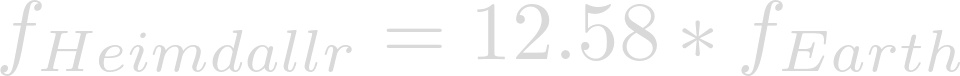
This change in momentum is a proportional to the change in velocity as well:

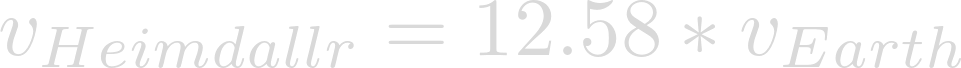
Wind speeds during Hurricane Katrina reached as much as 175mph. Plug that into our proportion.

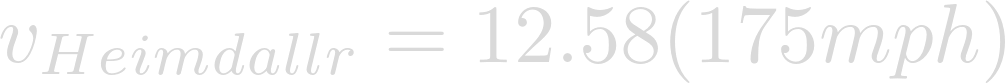
Finally evaluation yields the potential maximum wind speed of a Katrina-like storm on Heimdallr.

Heimdallr's immense rotational velocity unsurprisingly leads to a massively powerful Coriolis force. Cyclones on Heimdallr would be incredibly violent events and would be some of the most powerful storms in the universe.